Kelly Criterion

Introduction

The Kelly Criterion is a mathematical formula used to determine the optimal size of a series of bets. Developed by John L. Kelly Jr. in 1956, the criterion has been widely adopted in various fields, including finance and gambling, due to its ability to maximize long-term wealth growth while managing risk. This guide delves into the principles, applications, advantages, and criticisms of the Kelly Criterion.

The Origins of the Kelly Criterion

John L. Kelly Jr. and Information Theory

John L. Kelly Jr. was a scientist at Bell Labs who worked on information theory. His 1956 paper, "A New Interpretation of Information Rate," laid the foundation for the Kelly Criterion. The criterion was initially intended to address issues in signal processing, but its principles proved applicable to betting and investment strategies.

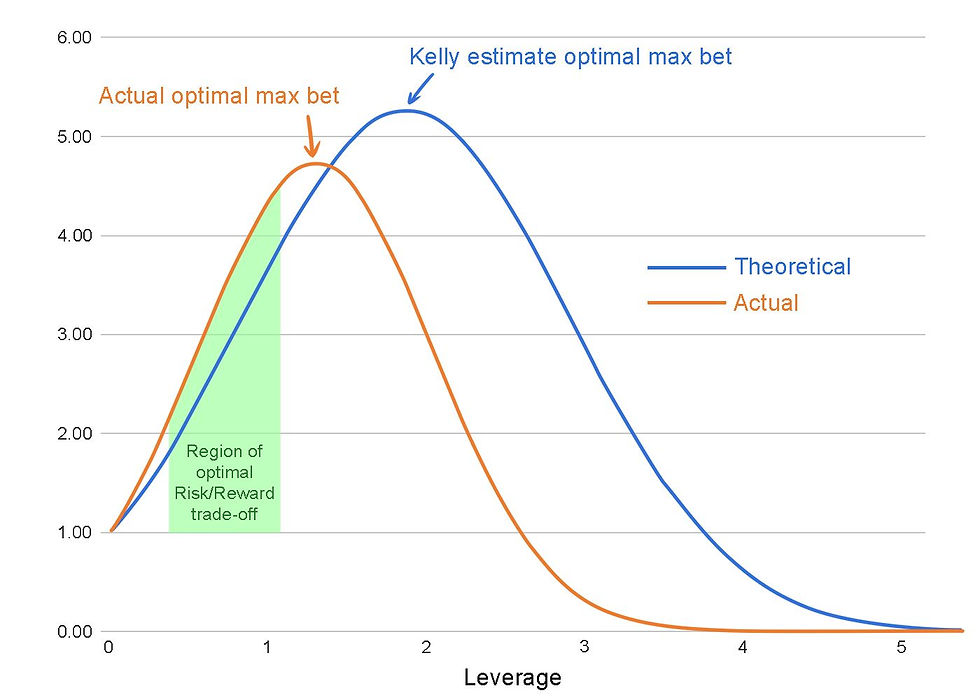
The Basic Formula

The Kelly Criterion formula is expressed as:

f∗=bp−qbf^* = \frac{bp - q}{b}f∗=bbp−q​

where:

• f∗f^*f∗ is the fraction of the current bankroll to wager.

• bbb is the multiple of the bet (i.e., the odds - 1).

• ppp is the probability of winning.

• qqq is the probability of losing (i.e., 1−p1 - p1−p).

This formula helps determine the optimal bet size to maximize logarithmic growth of wealth over time.

Principles of the Kelly Criterion

Maximizing Logarithmic Utility

The Kelly Criterion aims to maximize the logarithm of wealth, rather than linear wealth, to account for diminishing marginal utility of money. This approach ensures that the strategy remains consistent with risk aversion, as the logarithmic function penalizes large losses more severely than it rewards equivalent gains.

Optimal Growth Rate

By using the Kelly Criterion, bettors and investors can achieve the highest possible long-term growth rate of their capital. This optimal growth rate is achieved by balancing the trade-off between potential returns and the risk of substantial losses.

Application of the Kelly Criterion

Gambling

In gambling, the Kelly Criterion is used to determine the optimal size of each bet based on the edge and odds offered by the bookmaker. Here’s how it works:

1. Calculate the Edge: Determine the edge by estimating the probability of winning and the odds offered.

2. Apply the Kelly Formula: Use the Kelly formula to calculate the optimal bet size.

3. Place the Bet: Place the bet according to the calculated fraction of the bankroll.

Example

Assume a bettor has a bankroll of $1,000, and they believe they have a 60% chance of winning a bet with odds of 2:1.

• p=0.6p = 0.6p=0.6

• q=0.4q = 0.4q=0.4

• b=2−1=1b = 2 - 1 = 1b=2−1=1

Applying the Kelly formula:

f∗=(1×0.6)−0.41=0.2f^* = \frac{(1 \times 0.6) - 0.4}{1} = 0.2f∗=1(1×0.6)−0.4​=0.2

The bettor should wager 20% of their $1,000 bankroll, which is $200.

Financial Markets

In finance, the Kelly Criterion is used to determine the optimal allocation of capital to various investment opportunities. This involves assessing the expected return and the risk associated with each investment.

Example

An investor is considering two stocks:

• Stock A: Expected return of 8%, standard deviation of 5%

• Stock B: Expected return of 10%, standard deviation of 7%

The investor would use the Kelly Criterion to determine the optimal proportion of their portfolio to allocate to each stock, taking into account the expected returns and the risks.

Portfolio Management

In portfolio management, the Kelly Criterion can be extended to multiple assets, optimizing the allocation to maximize long-term growth while considering diversification and risk management.

Example

An investor has a portfolio with the following expected returns and risks:

• Asset 1: Expected return of 12%, risk of 8%

• Asset 2: Expected return of 10%, risk of 6%

• Asset 3: Expected return of 15%, risk of 10%

Using the Kelly Criterion, the investor can calculate the optimal allocation to each asset to achieve the maximum geometric growth rate for the portfolio.

Advantages of the Kelly Criterion

Maximizes Long-Term Growth

The primary advantage of the Kelly Criterion is its ability to maximize the long-term growth rate of wealth. By focusing on logarithmic utility, the criterion ensures that capital grows at the fastest possible rate while managing risk.

Risk Management

The Kelly Criterion inherently manages risk by adjusting the bet size based on the edge and the odds. This prevents overbetting and reduces the likelihood of catastrophic losses, ensuring that the bettor or investor can sustain their strategy over the long term.

Objective and Quantitative

The Kelly Criterion provides a clear, objective, and quantitative approach to decision-making. This eliminates guesswork and emotional biases, allowing for more disciplined and rational betting and investment strategies.

Criticisms and Limitations

Overestimation of Probabilities

One major criticism of the Kelly Criterion is the potential for overestimating probabilities. If the estimated probability of winning is too optimistic, the formula will recommend larger bet sizes, increasing the risk of significant losses.

Large Bet Sizes and Volatility

The Kelly Criterion can sometimes recommend large bet sizes, leading to high volatility in the short term. This can be uncomfortable for bettors and investors who prefer more stable returns. To address this, some practitioners use a "fractional Kelly" approach, betting a fixed fraction (e.g., half or a quarter) of the Kelly amount to reduce volatility.

Assumption of Unlimited Betting Opportunities

The Kelly Criterion assumes an infinite number of betting opportunities with independent outcomes. In reality, bettors and investors may face limited opportunities and correlated risks, which can affect the strategy's effectiveness.

Complexity and Practical Implementation

Implementing the Kelly Criterion requires accurate estimation of probabilities and odds, which can be challenging. Additionally, the criterion may not always be practical in real-world scenarios where liquidity, transaction costs, and other factors need to be considered.

Modifications and Variations

Fractional Kelly

To address the issue of high volatility, many practitioners use a fractional Kelly approach. This involves betting a fixed fraction (e.g., half or a quarter) of the Kelly amount. This reduces risk and volatility while still benefiting from the Kelly Criterion's principles.

Example

If the full Kelly bet size is 20% of the bankroll, using a half-Kelly approach would mean betting 10% of the bankroll.

Kelly Criterion for Multiple Bets

When dealing with multiple simultaneous bets or investments, the Kelly Criterion can be extended to allocate capital across different opportunities. This involves solving a system of equations to find the optimal allocation that maximizes the portfolio's overall growth rate.

Example

An investor has $10,000 to allocate between three stocks with the following expected returns and risks:

• Stock A: Expected return of 12%, risk of 8%

• Stock B: Expected return of 10%, risk of 6%

• Stock C: Expected return of 15%, risk of 10%

Using the Kelly Criterion for multiple bets, the investor can calculate the optimal allocation to each stock to maximize the portfolio's geometric growth rate.

Incorporating Transaction Costs and Taxes

In practice, transaction costs and taxes can significantly impact the effectiveness of the Kelly Criterion. Adjusting the formula to account for these factors can provide more accurate and practical recommendations.

Example

If the expected return is 10% but transaction costs reduce the net return to 8%, the Kelly formula should be adjusted to reflect this net return.

Practical Considerations

Accurate Estimation of Probabilities

The success of the Kelly Criterion depends on accurate estimation of probabilities and odds. Bettors and investors must conduct thorough research and use reliable data to make informed decisions.

Continuous Monitoring and Adjustment

Market conditions and probabilities can change over time. Continuous monitoring and adjustment of the Kelly bet sizes are necessary to maintain optimal performance.

Risk Tolerance and Personal Preferences

While the Kelly Criterion aims to maximize long-term growth, individual risk tolerance and preferences should be considered. Some may prefer a more conservative approach, using a fractional Kelly strategy to reduce risk and volatility.

Conclusion

The Kelly Criterion is a powerful tool for maximizing long-term wealth growth in both gambling and investment contexts. By determining the optimal bet size based on probabilities and odds, it offers a disciplined and quantitative approach to decision-making. However, its effectiveness depends on accurate estimation of probabilities, continuous monitoring, and consideration of practical factors such as transaction costs and personal risk tolerance.

Despite its limitations and criticisms, the Kelly Criterion remains a valuable strategy for those seeking to optimize their betting and investment outcomes. Whether used in full or in a fractional form, it provides a robust framework for managing risk and enhancing long-term profitability.